本記事では、『回帰不連続デザイン』について解説していきます。
専門すぎない範囲で、解説をします。もっと詳しく知りたい方は、本記事を読まれたあとより詳しい記事でお調べくださいm(_ _)m
はじめに
以前、データ解釈学の解説記事の一部で紹介した「回帰不連続デザイン」。
その書籍の中でしっかり理解することができませんでしたので、理解するために改めてまとめてみました。
まずはWikiのリンク貼っておきます。

腹立たしいほどに、回帰不連続デザインについて、一般的な言葉で語られた記述がないので、非常に理解に苦しみました。どう検索すれば良かったのでしょうか。
統計学が万人に受け入れられないのはこういうところだと思います。もっとわかりやすく表現しろい!!
さて、取り乱しました。概要を把握するのは以下の記事が良いと思いました。Pythonでやってくれいるのもでかいですね。(ずっと言っているけどこういう記事書けるようになりたい…)

次にこの記事もいい感じでした。
株式会社セールスアナリティクスという会社の記事だけあって、ビジネス分野での話もあり非常にわかりやすいですね。回帰不連続デザインについて調べるとわかりますが、医療分野や政治の分野での例などが多く、そんなものを例に出されても私は理解ができません!w
https://www.salesanalytics.co.jp/column/no00220/
さて、私は上記のようなわかりやすい平易な記事から、学問的な記事に踏み込んで理解を広げました。それを以下でまとめていきます。
極力平易な言葉で表現しますので、正確に統計的な意味を反映しきれていないかもしれません。その際はどうかご指摘をお願いいたします。
回帰不連続デザインとは、ざっくり解説
まず私がざっくり理解したのは、人為的な理由(赤点による補講や法律による飲酒の年齢制限)でとある事象の発生確率や件数に顕著な差が出てくるよ、ということです。
これの顕著な差を「回帰不連続デザイン」で検証するというものです。
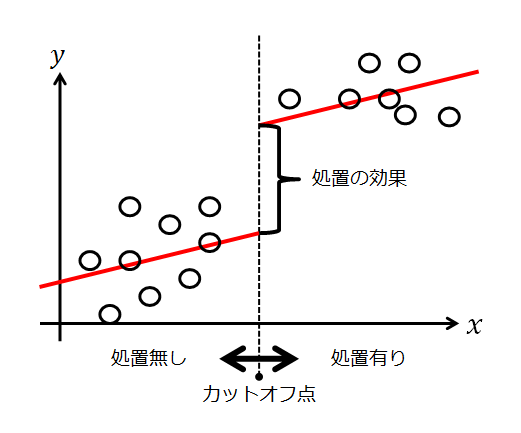
「この差をちゃんと検証する」というようなイメージです。
これだけ見ると、わかりやすい。でも調べると学問的でややこしい。きっとここに「面白さ」があるだろうという期待感が持てますね。
どういう時に使われるのか
では次に、どういう時に使われるかを見ていきます。同じくwikiから内容を拝借します。
回帰不連続デザインの背後にある直観的な考え方は成績優秀者向けの奨学金の評価を検討することでよく表現できる。このような介入の因果効果の測定に関する主要な問題は、処置の割り当ての内生性である。評価の高い学生は成績優秀者向け奨学金を得ると同時に優秀な成績を残すであろうから、成績優秀者向け奨学金を得た人とそうでない人の成績を比較することは、推定における上方バイアスを導くだろう。成績優秀者向け奨学金が成績を全く向上させないとしても、奨学金を得た人は奨学金を貰わなかった人よりよいパフォーマンスを見せるだろう。なぜならば単純に事前に成績の良かった生徒に対して奨学金が与えられるからである。
実験デザインが無いのにも関わらず、回帰不連続デザインは因果効果を取り出すために介入の外生的な特徴を利用することができる。もしある特定の成績-例えば80%以上-を残した生徒すべてに奨学金が与えられるのであれば、80%のカットオフ点付近の生徒を比較することで局所的処置効果を取り出すことが出来る。これは直感的には、成績が79%だった生徒は成績が81%だった生徒と非常に似ているが、しかしながら事前に決められた閾値80%が与えられた下で、片方の生徒は奨学金を得られない一方でもう一方の生徒は奨学金が得られる。奨学金を得られた生徒(処置群)の成績と奨学金を得られなかった生徒(対照群)の処置がなされなかった(英: counterfactual)成績を比較することで、局所的な処置効果が取り出される
この日本語の日本語訳をしていきます。
まずは私が初見で理解できなかった、わかりにくい単語の解説です。
- 介入の因果効果
落ち着けばわかりますよね。ただ、この文章の中にいると難解に聞こえてしまう。
この文章では、介入(奨学金を与える)の因果効果(奨学金が原因で成績が向上したかどうか)になります。 - 処置の割り当ての内生性
処置(奨学金を出す出さない)の割り当て(誰に出すか)の内生性(出す出さないの決定に相関関係などがないか(もしくはランダムでない抽出か)など)
まず、内生性という言葉は計量経済学の学問用語だそうです。
(内生性Wiki)
計量経済モデルにおいて、説明変数と誤差項との間に相関があるときに、内生性(endogeneity)があるという。このとき、説明変数は内生的(endogenous)であることになる。説明変数が内生的であれば、推定されたパラメータは一致推定量ではなくなり、推定値は統計学的に信頼されるものとはなりえない。
ということは、今回の例でいくと、説明変数(高得点者)と誤差項(回帰モデル内に含まれていない要因に起因するバラツキ=奨学金による奨励)。間違いなく、相関がありますね。
本文に戻って、「介入の因果効果の測定に関する主要な問題は、処置の割り当ての内生性である。」処置の割り当てを得点によって決めていますから、当然内生性が発生します。(逆に内生性がないというのは、ランダム抽出などだと思います。)ここが因果推論の主たる論点だといっているようです。
と思っていたのですが、違う気がしてきました。あとから編集しますので、一旦これで!w
- 外生的な特徴
内生的の対義語。独立している、というようなイメージ。 - カットオフ点
閾値のこと - 局所的処置効果
局所的(閾値前後の僅かに奨学金取れなかった人たちと、ギリギリ奨学金取れた人たち)処理(奨学金を出す出さない)効果(成績どうよ) - 処置群/対照群
奨学金を出したか出さないかのこと。処置群はギリギリ奨学金をもらい、対照群はあと少しで奨学金をもらえなかった人たちのこと。
日本語の日本語訳って難しいですね。
さて、本文を再度見ていただいて、どういう時に使えるかわかりましたか?
つまり、当落線上の人たちを比較して、その後どうかを見る、というイメージです。
わかりやすく説明すると
| 対照群 | 処置群 | |
|---|---|---|
| フランスW杯 | 三浦知良 | 小野伸二 |
| 日韓W杯 | 中村俊輔 | 中山雅史 |
| ドイツW杯 | 久保竜彦 | 巻誠一郎 |
| 南アフリカW杯 | 香川真司 | 矢野貴章 |
| ブラジルW杯 | 該当者なし | 大久保嘉人 |
| ロシアW杯 | 該当者なし | 該当者なし |
こんな感じですね〜。最近は「外れるのはカズ、三浦カズ」「タマダ……マキ」とかなくなりましたね。悲しき。
話逸らしました。すみません。
こういうような人たちを比較していく、という感じです。
回帰不連続デザインの二つの手法
回帰不連続デザインでは、主に二つの手法があるようです。それは「パラメトリック」と「ノンパラメトリック」になります。
ちょっと不安になってきたので、「パラメトリック」と「ノンパラメトリック」ってなんだっけ?ということで調べ直しました。
簡単に言うと、「パラメトリック」は調べたい集団の母集団の分布が正規分布していると考えられるものに対して、「ノンパラメトリック」はとりあえず仮定がない、情報がない集団に対してアプローチできる手法だそうです。
パラメトリックな手法
こちらは基本的に重回帰分析できるようなものなので、説明を割愛します。
ノンパラメトリックな手法
こんな感じに線形回帰式になります。
$$Y=α+τD+β_{1}(X-c)+β_{2}D(X-c)+ε$$
それぞれ前提や条件があって、
① c – h ≦ X ≦ c + h
②cは処置のカットオフ点
③Dは X ≥ c ならば1、X ≤ c ならば0であるバイナリ変数
④hはデータバンド幅
要するに、cを境に、二つの線形回帰式ができますよ。そしてその傾きと切片は異なりますよってことになります。
実務で使っていったり、これ以上の深い理解を得るには、さらにこれ以上知る必要があると思いますが、引き出しを増やしていく上では、この程度の理解でいいのかなーと思っています。
以上、「回帰不連続デザイン」についてでした。統計学的な側面の質問以外でしたらお受けできますので、お知らせください。
それでは。






コメント