書籍メモとして、備忘録です。
【書籍情報】
書籍名:分析者のためのデータ解釈学入門 データの本質を捉える技術
著者:江崎貴裕
出版社:ソシム
第9章 多変量データを解釈する
探索的分析と多重検定
探索的分析とは、データから特徴を見出すことを目的とした分析のこと。個人的には業務で基礎分析などと言ったりしていました。
この探索的分析は、やることは簡単かもしれませんが、インサイトを得ることができるかというとそうでもなかったり、分かりきっているような内容しか情報が得られなかったりなど、難しさもあります。
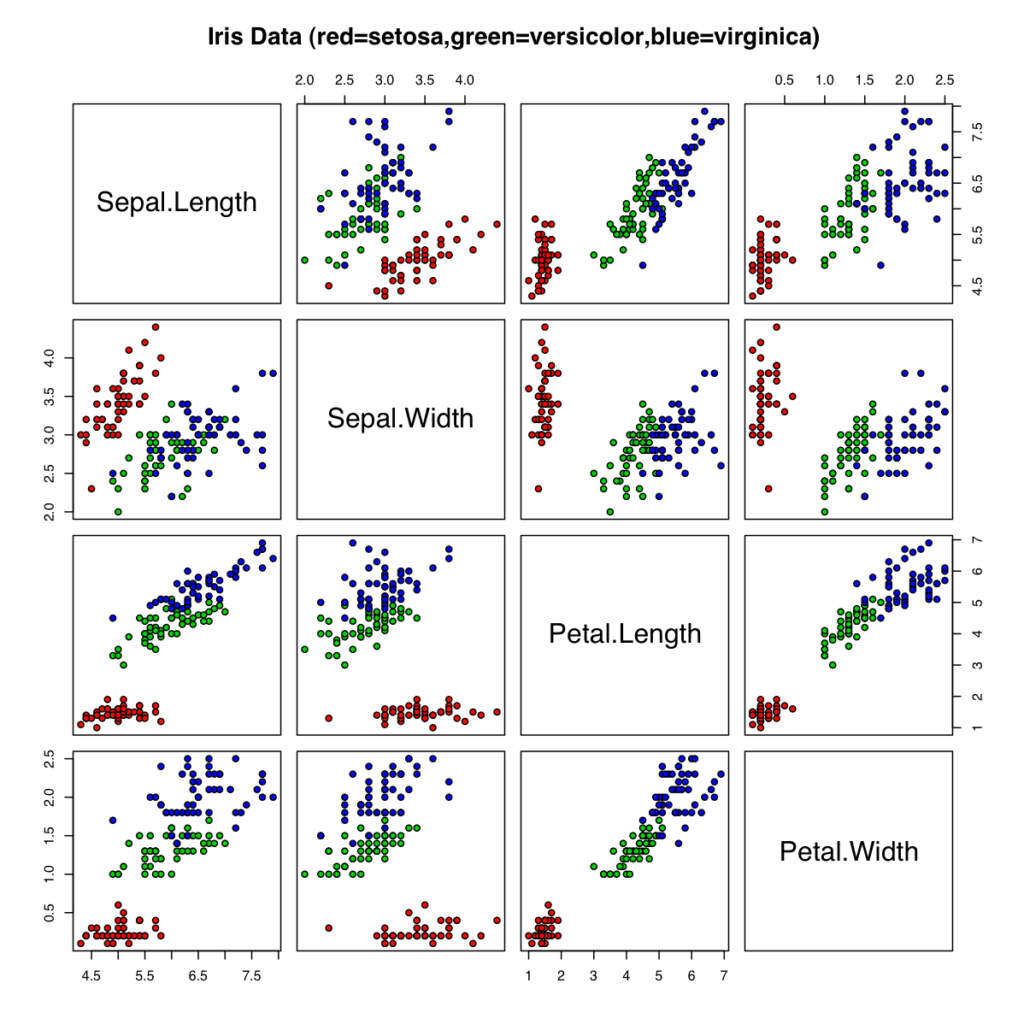
こんな感じで散布図を網羅的に表示させることで、比較的容易に特徴を見つけ出すことも可能になる。
次に検定の多重性を見ていきます。
検定の多重性とは、仮設検定を何度も繰り返すことで発生する問題のことで、それは何回もやれば「たまたま」が1回でも発生する確率も上昇する。
検定の多重性を補正するやり方としてポピュラーのものとしては、「Bonferroni法」というものがあり、これは検定の回数nで有意水準を割ったものを採用するという方法のこと。
他にもHolm法という方法もある。
相関の構造を探る
偏相関係数
偏相関係数とは、本当は関係のない2つの要因を炙り出す方法。
①XとYとZの関係性があるとする。
②XとYの相関係数は比較的高い。
③しかし、どうにも信憑性のない要因同士(XとY)だとする。
④この時見かけの相関が発生していると考えられる。
⑤その要因となっているのがZだと仮定する。
⑥そのZの要素を除いてXとYの相関関係を見たい。
⑦偏相関係数による計算によってXとYの関係性を定量的に計ることができる。
主成分分析
※省略
クラスタリング
※省略
第10章 数理モデリングの要点
「数理モデリング」は何をやっているのか
数理モデルとは
データにおける変数の振る舞いや関係性を数理的な表現で模擬したもの
この原点に立って以下展開します。
数理モデルは、一般的に3つの構成要素があり、それぞれ「変数」「数理構造」「パラメータ」から構成されます。簡単に言うと数式で表せると言うイメージで概ね問題ないと思います。
これらの構成要素から作られた数理モデルは妥当性を検討しないといけません。妥当性の検証は以下の項目などから検討する必要があります。
①モデル構築に使ったデータを説明できるか(適合度や決定係数など)
②未知のデータを説明できるか(過学習など)
③論理的妥当性があるか(現実の事象に即しているか)
モデルによる「予測」
モデルによる予測については、「予測しやすい問題」と「予測しにくい問題」があることを理解する必要があります。
また、大きく外れた予測値を出すことはこんなんで、極端な事象を予測することが困難になります。
それぞれのモデルの特性とその目的を吟味して、モデルを活用しましょう。
以上。
コチラもどうぞ

ttps://zizou-book-lab.com/data_interpretation_1to3/
ttps://zizou-book-lab.com/data_interpretation_4to5/





コメント